可解释性-积分梯度算法（Integrated Gradients）

最近阅读文章看到一篇可解释性的相关的，往上追溯到了积分梯度算法（Integrated Gradients），蛮有意思，写篇博客整理一下思路 参考论文：Axiomatic Attribution for Deep Networks https://arxiv.org/abs/1703.01365

motivation

这篇文章研究的是如何将模型的预测归因到模型的输入上，以对模型进行debug、提取规则以更好的使用模型。 先前的基于经验的归因评估方法，例如通过归因挑选Top k个像素，随机变化其值然后衡量得分下降的幅度。但是这种方法不够自然，因为模型可能没见过变化后的图像因此给出一个较低的得分。其他的经验评估技术都无法区分源于扰动数据的伪影、行为不当的模型和行为不当的归因方法。 因此本篇文章基于两个基本公理：Sensitivity和Implementation Invariance来设计自己的归因方法。

两个基本公理

Sensitivity

对于每个输入而言，如果baseline和与其在一个特征和预测值上不相同，那么这个特征应该被给予一个非零的归因。 用梯度作为归因，和Sensitivity是相违背的，例如函数\(f(x) = 1 - ReLU(1-x) = \[ f(x) = \begin{cases} x & \text{if } x < 1 \\ 0 & \text{otherwise} \end{cases} \]\) 当x大于等于1时，尽管此时的x与baseline不同，但是其梯度（即归因）为零。因此以梯度作为归因会导致focus到一些不相关的特征

Implementation Invariance

对于两个在功能上等价的神经网络（输入相同时网络输出相同，但实现方法可能不同），他们对于同一输入的归因也必须是相同的。 而基于梯度的归因是依赖于网络具体实现的，不满足该性质。

Our Method：Integrated Gradients

该方法不直接使用梯度，而是对梯度进行积分。对于输入x和baseline x’，沿着第i维的积分梯度定义如下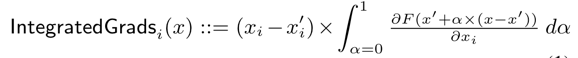： 实际计算时选择一个路径进行积分，该论文选择直线，即 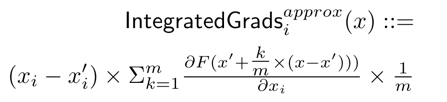比较容易证明，这个方法是满足上面两个公理的 实验也发现，效果挺不错的，不愧是被引4000+的文章

算法核心代码大致如下：

def _compute_ig(sess, input_tensors, embedding_tensor,
                gradient_tensor, output_tensor, transformed_input_df,
                baseline_df, num_reps):
    batch_size = 20  # keep small enough to ensure that we do not run out of
    # memory
    num_reps = num_reps

    tensor_values = sess.run(embedding_tensor,
                             _get_feed_dict(input_tensors,
                                            transformed_input_df))

    tensor_baseline_values = sess.run(embedding_tensor,
        _get_feed_dict(input_tensors, baseline_df))

    # 计算
    scaled_embeddings = _get_scaled_inputs(tensor_values[0],
                                           tensor_baseline_values[0],
                                           batch_size, num_reps)
    scaled_input_feed = {}
    for key, tensor_info in input_tensors.items():
        scaled_input_feed[
            get_tensor(sess, tensor_info.name)] = _get_unscaled_inputs(
            transformed_input_df[key][0], batch_size)

    scores = []
    path_gradients = []

    # 积分值估计计算
    for i in range(num_reps):
        scaled_input_feed[embedding_tensor] = scaled_embeddings[i]
        path_gradients_rep, scores_rep = sess.run(
            [gradient_tensor, output_tensor[:, 1]], scaled_input_feed)
        path_gradients.append(path_gradients_rep[0])
        scores.append(scores_rep)

    baseline_prediction = scores[0][
        0]  # first score is the baseline prediction
    prediction = scores[-1][-1]  # last score is the input prediction

    # integrating the gradients and multiplying with the difference of the
    # baseline and input.
    ig = np.concatenate(path_gradients, axis=0)
    integral = _calculate_integral(ig)
    integrated_gradients = (tensor_values[0] - tensor_baseline_values[
        0]) * integral
    integrated_gradients = np.sum(integrated_gradients, axis=-1)

    return integrated_gradients, baseline_prediction, prediction

# 获取积分路径中各点
def _get_scaled_inputs(input_val, baseline_val, batch_size, num_reps):
    list_scaled_embeddings = []
    scaled_embeddings = \
        [baseline_val + (float(i) / (num_reps * batch_size - 1)) *
         (input_val - baseline_val) for i in range(0, num_reps * batch_size)]

    for i in range(num_reps):
        list_scaled_embeddings.append(
            np.array(scaled_embeddings[i * batch_size:i * batch_size +
                                                      batch_size]))

    return list_scaled_embeddings