Post

BERT复现-旋转位置编码RoPE

Posted
By zhizhou 8 min read

旋转位置编码，来源于文章（ROFORMER: ENHANCED TRANSFORMER WITH ROTARY POSITION EMBEDDING），是一种通过构造特定的绝对位置编码使得相对位置信息能够介入到attention中去的一种技术 RoPE在LLAMA、PaLM等模型中得到了应用。 不过笔者在对比中发现，META Github仓库中的RoPE实现、Huggingface LLAMA中的RoPE实现、Huggingface Roformer中的RoPE实现竟然均不相同，代码上其实是有所不同的（不知道是有意修改还是无意写错），下面将详细介绍

RoPE原理

引用Roformer中比较精髓的一句话：

Specifically, the proposed RoPE encodes the absolute position with a rotation matrix and meanwhile incorporates the explicit relative position dependency in self-attention formulation.

特别的，提出的RoPE方法引入了旋转矩阵来编码绝对位置信息，与此同时隐式的在自注意力机制中引入了相对位置信息

具体是怎么做的呢，首先先看传统的Transformer的做法, 用x表示token embedding，q、k、v分别表示queries, keys, and value representations. f就是一个将token embedding和位置m（n）编码为qkv表示的一个函数 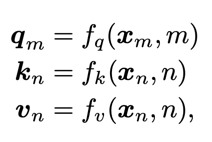img.png

在传统的Transformer里呢，f做的就是把token embedding加上sinusoidal function形式的绝对位置编码p，然后通过一个线性层（即一个矩阵W）映射到qkv表示的空间 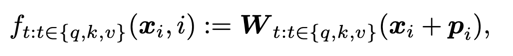img.png

这篇论文的动机其实很难评价，作者在论文的Conclusion部分也说了，相对位置编码可以work这件事很难解释，而且作者苏神在知乎上写了这么一段话： img.png 然后这篇论文其实也未真正发表，甚至作者自己都不知道motivation该怎么写，但这个方法可能确实work吧，所以大家都用了 （其实写到这里我都快不想写这篇博客了，未发表的论文感觉还是有点难评价，不够成熟） 参见：https://www.zhihu.com/question/450936573/answer/1797187035

作者的想法就是，改一下这个f的形式（其实就相当于，每对x_i, x_i+1都进行一次在复数极坐标系中的旋转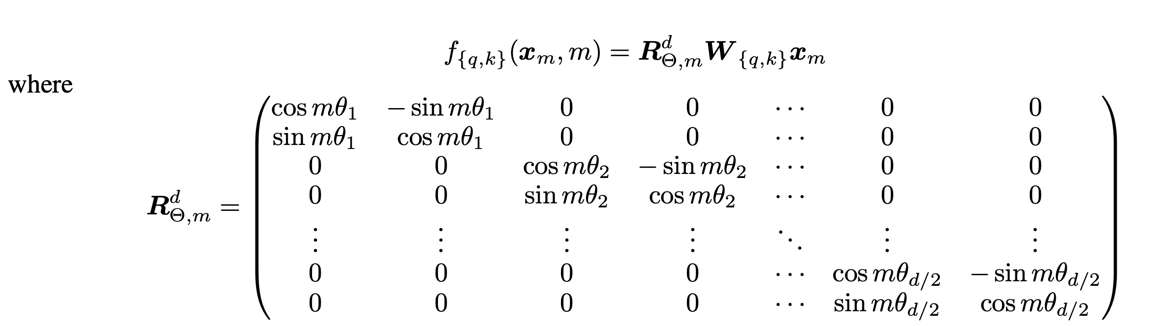）： img.png 具体细节后续补充，挖个坑先。 然后这个f就可以等价于这个形式，这就是RoPE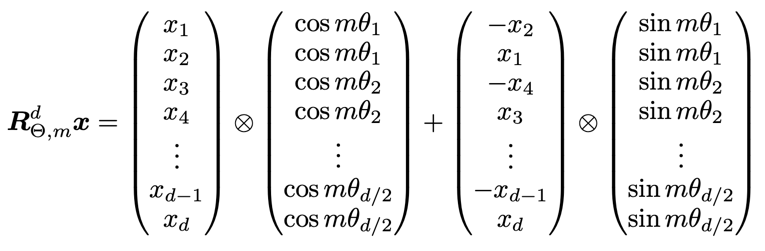 img.png

RoPE实现

我发现RoPE有三种不同的代码实现，很奇怪，下面一一介绍

第一种是META的LLAMA（ https://github.com/facebookresearch/llama ）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

import torch
from typing import Tuple
def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):
    freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
    t = torch.arange(end, device=freqs.device)  # type: ignore
    freqs = torch.outer(t, freqs).float()  # type: ignore
    freqs_cis = torch.polar(torch.ones_like(freqs), freqs)  # complex64
    return freqs_cis


def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):
    ndim = x.ndim
    assert 0 <= 1 < ndim
    assert freqs_cis.shape == (x.shape[1], x.shape[-1])
    shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
    return freqs_cis.view(*shape)


def apply_rotary_emb(
    xq: torch.Tensor,
    xk: torch.Tensor,
    freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
    xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
    xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
    freqs_cis = reshape_for_broadcast(freqs_cis, xq_)
    xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)
    xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)
    return xq_out.type_as(xq), xk_out.type_as(xk)

# 获取修改后的query、key
freqs = precompute_freqs_cis(head_dim, seq_len)
xq_meta_llama, xk_meta_pyllama = apply_rotary_emb(xq, xk, freqs_cis=freqs)

相当于只要了原文中的第一项，即（x_1, …, x_d） * (cos(mtheta1), …, cos(mthetad/2))

第二种是huggingface里的LLAMA实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

import torch
class RotaryEmbedding(torch.nn.Module):
    def __init__(self, dim, max_position_embeddings=2048, base=10000, device=None):
        super().__init__()
        inv_freq = 1.0 / (base ** (torch.arange(0, dim, 2).float().to(device) / dim))
        self.register_buffer("inv_freq", inv_freq)

        # Build here to make `torch.jit.trace` work.
        self.max_seq_len_cached = max_position_embeddings
        t = torch.arange(
            self.max_seq_len_cached,
            device=self.inv_freq.device,
            dtype=self.inv_freq.dtype,
        )
        freqs = torch.einsum("i,j->ij", t, self.inv_freq)
        # Different from paper, but it uses a different permutation in order to obtain the same calculation
        emb = torch.cat((freqs, freqs), dim=-1)
        self.cos_cached = emb.cos()[None, None, :, :]
        self.sin_cached = emb.sin()[None, None, :, :]

    def forward(self, x, seq_len=None):
        # x: [bs, num_attention_heads, seq_len, head_size]
        # This `if` block is unlikely to be run after we build sin/cos in `__init__`. Keep the logic here just in case.
        if seq_len > self.max_seq_len_cached:
            self.max_seq_len_cached = seq_len
            t = torch.arange(
                self.max_seq_len_cached, device=x.device, dtype=self.inv_freq.dtype
            )
            freqs = torch.einsum("i,j->ij", t, self.inv_freq)
            # Different from paper, but it uses a different permutation in order to obtain the same calculation
            emb = torch.cat((freqs, freqs), dim=-1).to(x.device)
            self.cos_cached = emb.cos()[None, None, :, :].to(dtype=x.dtype)
            self.sin_cached = emb.sin()[None, None, :, :].to(dtype=x.dtype)
        return (
            self.cos_cached[:, :, :seq_len, ...].to(dtype=x.dtype, device=x.device),
            self.sin_cached[:, :, :seq_len, ...].to(dtype=x.dtype, device=x.device),
        )


def rotate_half(x):
    """Rotates half the hidden dims of the input."""
    x1 = x[..., : x.shape[-1] // 2]
    x2 = x[..., x.shape[-1] // 2 :]
    print(x1)
    print(x2)
    print(torch.cat((-x2, x1), dim=-1))
    return torch.cat((-x2, x1), dim=-1)


def apply_rotary_pos_emb(q, k, cos, sin, offset: int = 0):
    cos = cos[..., offset : q.shape[-2] + offset, :]
    sin = sin[..., offset : q.shape[-2] + offset, :]
    q_embed = (q * cos) + (rotate_half(q) * sin)
    k_embed = (k * cos) + (rotate_half(k) * sin)
    return q_embed, k_embed

相当于第二项变成了（x_1, …x_d/2, -x_d/2, …, -x_d） * (cos(mtheta1), …, cos(mthetad/2))

最后一种就是 huggingface中的Roformer了, 与原文公式一致

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

def apply_rotary_position_embeddings(sinusoidal_pos, query_layer, key_layer, value_layer=None):
    # https://kexue.fm/archives/8265
    # sin [batch_size, num_heads, sequence_length, embed_size_per_head//2]
    # cos [batch_size, num_heads, sequence_length, embed_size_per_head//2]
    sin, cos = sinusoidal_pos.chunk(2, dim=-1)
    # sin [θ0,θ1,θ2......θd/2-1] -> sin_pos [θ0,θ0,θ1,θ1,θ2,θ2......θd/2-1,θd/2-1]
    sin_pos = torch.stack([sin, sin], dim=-1).reshape_as(sinusoidal_pos)
    # cos [θ0,θ1,θ2......θd/2-1] -> cos_pos [θ0,θ0,θ1,θ1,θ2,θ2......θd/2-1,θd/2-1]
    cos_pos = torch.stack([cos, cos], dim=-1).reshape_as(sinusoidal_pos)
    # rotate_half_query_layer [-q1,q0,-q3,q2......,-qd-1,qd-2]
    rotate_half_query_layer = torch.stack([-query_layer[..., 1::2], query_layer[..., ::2]], dim=-1).reshape_as(
        query_layer
    )
    query_layer = query_layer * cos_pos + rotate_half_query_layer * sin_pos
    # rotate_half_key_layer [-k1,k0,-k3,k2......,-kd-1,kd-2]
    rotate_half_key_layer = torch.stack([-key_layer[..., 1::2], key_layer[..., ::2]], dim=-1).reshape_as(key_layer)
    key_layer = key_layer * cos_pos + rotate_half_key_layer * sin_pos
    if value_layer is not None:
        # rotate_half_value_layer [-v1,v0,-v3,v2......,-vd-1,vd-2]
        rotate_half_value_layer = torch.stack([-value_layer[..., 1::2], value_layer[..., ::2]], dim=-1).reshape_as(
            value_layer
        )
        value_layer = value_layer * cos_pos + rotate_half_value_layer * sin_pos
        return query_layer, key_layer, value_layer
    return query_layer, key_layer

class RoFormerSinusoidalPositionalEmbedding(nn.Embedding):
    """This module produces sinusoidal positional embeddings of any length."""

    def __init__(self, num_positions: int, embedding_dim: int, padding_idx: Optional[int] = None) -> None:
        super().__init__(num_positions, embedding_dim)
        self.weight = self._init_weight(self.weight)

    @staticmethod
    def _init_weight(out: nn.Parameter) -> nn.Parameter:
        """
        Identical to the XLM create_sinusoidal_embeddings except features are not interleaved. The cos features are in
        the 2nd half of the vector. [dim // 2:]
        """
        n_pos, dim = out.shape
        position_enc = np.array(
            [[pos / np.power(10000, 2 * (j // 2) / dim) for j in range(dim)] for pos in range(n_pos)]
        )
        out.requires_grad = False  # set early to avoid an error in pytorch-1.8+
        sentinel = dim // 2 if dim % 2 == 0 else (dim // 2) + 1
        out[:, 0:sentinel] = torch.FloatTensor(np.sin(position_enc[:, 0::2]))
        out[:, sentinel:] = torch.FloatTensor(np.cos(position_enc[:, 1::2]))
        out.detach_()
        return out

    @torch.no_grad()
    def forward(self, input_ids_shape: torch.Size, past_key_values_length: int = 0) -> torch.Tensor:
        """`input_ids_shape` is expected to be [bsz x seqlen]."""
        bsz, seq_len = input_ids_shape[:2]
        positions = torch.arange(
            past_key_values_length, past_key_values_length + seq_len, dtype=torch.long, device=self.weight.device
        )
        return super().forward(positions)
LLAMA RoPE
This post is licensed under CC BY 4.0 by the author.